O que é o Softmax?

O que é o Softmax, para que serve, e quais as vantagens em relação a outras técnicas?

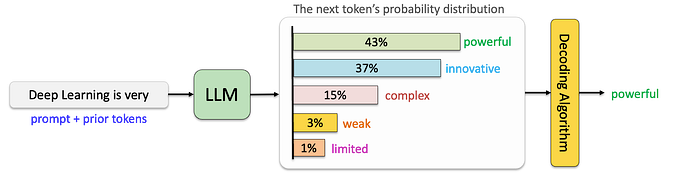
O Softmax costuma ser utilizado na última camada de uma rede neural, quando temos um problema multiclasse.

Um problema é multiclasse quando temos que classificar o input em alguma das classes de saída possíveis. Por exemplo, o vetor de entrada é uma imagem contendo um único animal, e a saída é o reconhecimento de um dentre os quatro animais a seguir: [cachorro, gato, cavalo, porco]. Queremos, dada uma imagem, saber qual a probabilidade de conter cada um dos animais dados.

Ou seja, o softmax é uma função que converte um vetor de números em probabilidades.

Note que o vetor de entrada pode conter qualquer número (de -infinito a +infinito), enquanto a saída é um vetor de probabilidades, então o mínimo de cada elemento deve ser zero e a soma de todos os elementos deve ser igual a 1.

Sempre me perguntei. Porque não fazer uma normalização simples, que equivale a somar todos os valores e dividir o valor pela soma? É a forma comum de transformar um vetor em probabilidades.

Bom, primeiro, vamos começar pela definição do softmax.

Definição do softmax

A seguir, uma explicação passo a passo da função.

Entrada de Dados: A função recebe como entrada um vetor de números chamado de logits. Esses logits representam as pontuações ou valores de saída de uma rede neural, antes de serem transformados em probabilidades.

Função Exponencial: Cada valor do vetor de logits é elevado à potência do número de Euler (constante matemática igual a 2,718…), tornando todos os valores positivos. Isto é feito pela função exponencial dada a seguir.

Por exemplo, se tivermos um vetor de logits [2, 1, 5, -1], após a aplicação da função exponencial em cada elemento, teremos

[7.39, 2.72, 148.41, 0.37]

Essa conta pode ser feita no Python, utilizando o código seguinte.

import math def exponencial(v):

#Recebe uma lista v de entrada

#Tira exp(x) de cada elemento x da lista

expx = [math.exp(x) for x in v]

return(expx)

Obs. Note que os valores negativos se tornaram positivos.

Normalização: Para transformar esses valores em probabilidades, é necessário normalizá-los. Isso é feito dividindo cada valor exponencial pela soma de todos os valores exponenciais. Dessa forma, cada valor no vetor resultante estará na faixa de 0 a 1, e a soma de todos os valores será igual a 1, o que é uma característica essencial para representar probabilidades.

Adaptando o código anterior, para calcular a função softmax completa:

import math def softmax(v): #Recebe uma lista v de entrada #Tira exp(x) de cada elemento x da lista expx = [math.exp(x) for x in v] somaexp = sum(expx) #Retorna exp(xi)/soma(exp(x)) return( [y/somaexp for y in expx])

Por exemplo, para o vetor de logits [2, 1, 5, -1], temos, após a aplicação do softmax:

[0.05, 0.02, 0.93, 0.00]

Neste caso, se o vetor de saída representar [cachorro, gato, cavalo, porco], quer dizer que há 93% de chance de a foto ser um cavalo, 5% de ser um cachorro e 2% de ser um gato.

Note que cada número é maior do que zero, e a soma do vetor é igual a um.

Interpretação

O softmax é uma simplificação de “softargmax”, algo como “aproximação do argumento máximo”. Em outras palavras, é uma aproximação do efeito “o vencedor leva tudo”.

A função exponencial tem uma curva como a seguinte. Valores negativos são maiores que zero, porém, muito pequenos. Já valores de entrada maiores do que zero, ficam ainda maiores após passarem pela função, pela característica exponencial da mesma. Portanto, o softmax transforma qualquer número real (de -infinito a +infinito) num valor positivo, e privilegia o maior valor.

Algumas diferenças em relação a uma normalização simples: essa só é válida para valores positivos, e por ser linear, o maior valor não vai ter diferença tão acentuada quanto seria no caso exponencial.

Exemplo:

Aumentando um pouquinho o maior valor do vetor de logits, [2, 1, 7, -1], temos o seguinte resultado no softmax:

[0.00667, 0.002455, 0.99053, 0.00033]

Note como o softmax privilegia o maior valor, dando a ele 99% de chance, contra menos de 1% dos demais.

Se aplicássemos uma normalização simples (dividir o vetor pela soma dos elementos), teríamos:

[0.22, 0.11, 0.77, -0.11]

Primeiro, nem faz sentido ter valor negativo numa probabilidade. Segunda característica, teríamos 77% para o maior valor, seguido de 22% para o segundo, ou seja, sem privilegiar o maior valor de forma acentuada.

Ué, mas aí o leitor esperto vai perguntar. Por que não utilizar diretamente a função argmax? Ou seja, sempre escolha direto o maior valor e pronto, eu não precisaria ficar fazendo esse monte de contas. Qual o problema dessa abordagem? Um minuto para pensar.

Pensou? O problema é que uma função como o máximo não é diferenciável.

Uma terceira característica do softmax é ser diferenciável (lembra das aulas de cálculo?). Tal característica é bem importante por conta do backpropagation, operação realizada para treinamento do modelo da rede neural. A derivada permite cálculo dos gradientes, dessa forma informando às camadas anteriores o quanto os seus pesos devem crescer ou decrescer, assim treinando a rede.

Outra reflexão. O softmax é muito utilizado, porém não é a única função possível — nada impede de criarmos outras variações. Digamos, poderíamos usar base 10 ao invés de utilizar base e. Qual seria o efeito disso? Ora, estaríamos privilegiando ainda mais o maior valor, pela função exponencial base 10 crescer mais rápido ainda do que a com base e. Se utilizássemos um valor menor do que e, seria o oposto, valores menores teriam maior probabilidade no final.

Portanto, eis as características do softmax: transforma números negativos em positivos, retorna um vetor de probabilidades somando 1, privilegia o maior valor e é diferenciável.

Assim vamos, pedacinho por pedacinho, entendendo a nossa rede neural.

Autores

Arnaldo Gunzi. Engenheiro pelo Instituto Tecnológico de Aeronáutica, Mestre em Eletrônica pela UFRJ e MBA em Gerência de Projetos pela FGV. Atua como coordenador de Projetos Analíticos na Klabin, liderando projetos em Advanced Analytics, AI e Quantum Computing e também é professor de Estatística, Cálculo e Otimização na XP Educação.

Ernée Kozyreff Filho é engenheiro formado no Instituto Tecnológico de Aeronáutica (ITA). Possui mestrado em Matemática e doutorado em Engenharia de Produção pela Texas Tech University, EUA. Foi professor em escolas de ensino fundamental, médio e superior, onde ministrou diversas disciplinas na área de exatas. Atualmente desenvolve modelos de otimização matemática para melhorar a eficiência de processos industriais na Klabin S.A.

Originally published at https://ideiasesquecidas.com on April 29, 2024.